bullet_solver

Barrel angle solver

Overview

In practice, the target to be hit is often moving, and the bullet is subject to resistance in the air and delay in the barrel firing. We need to build a barrel angle solver to predict the firing angle of the barrel to achieve more accurate strikes.

Objective:

• Consider air resistance (proportional to velocity)
• Consider target velocity
• Consider firing delay

Difficulty.

• No resolution
• Target solving frequency greater than 1Khz

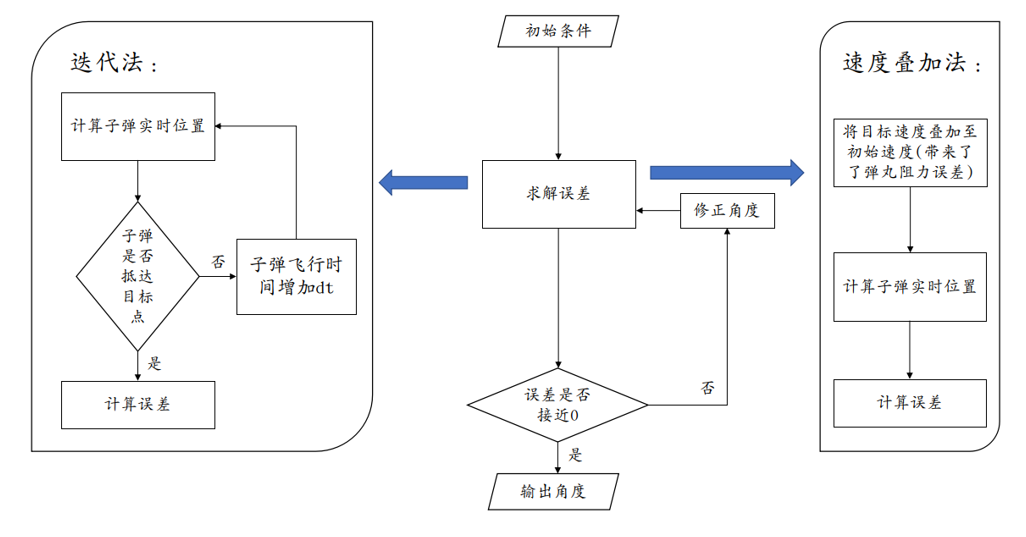
Two algorithms.

• Iterative method
  • Advantages: high accuracy (when iterations are high)
  • Disadvantage: slow speed
• Speed superposition method
  • Advantages: fast (within 20 us)
  • Disadvantage: inherent error exists
    
• Block diagram of the algorithm.

Model derivation

Air resistance is proportional to velocity, and the target point moves with constant velocity 2D bullet motion model: In the xz plane, the actual position of the bullet corresponds to a vector in the xoz plane, assuming that the bullet bullet launch point is the coordinate origin. 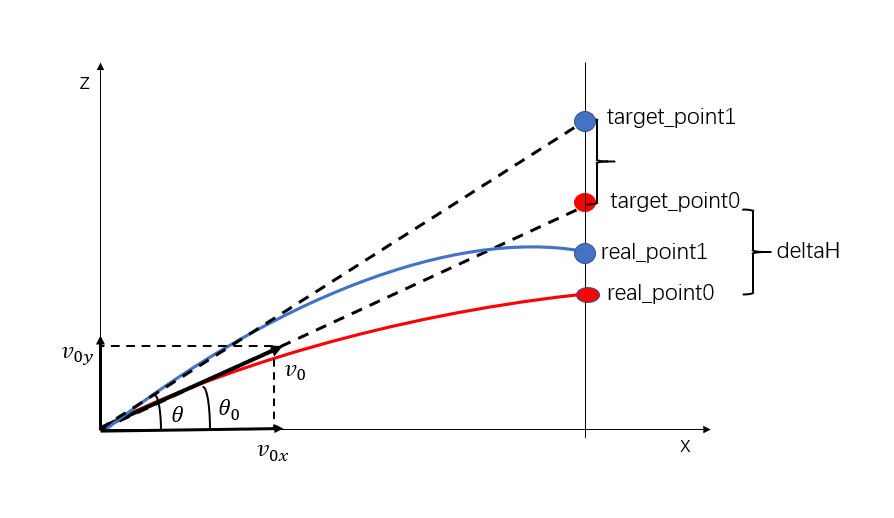Denote by x the component of the bullet position vector in the x-axis direction, and by z the component of the bullet position vector in the z-axis direction; $v_0$ denotes the initial velocity of the bullet launch, $v_x, v_z$ denote the components of the bullet velocity in the x-axis and z-axis, $v_{x_0}, v_{z_0}$ denote the components of $v_0$ in the x-axis and z-axis, respectively, k is the air resistance coefficient, g is the acceleration of gravity, m denotes the weight of the bullet, $f_x$$ denotes the component of the air resistance to the bullet in the x-direction, and according to the physical knowledge we know that

$$f_x=-kv_x=m\frac{dv_x}{dt}\tag{1}$$

Organizing equation (1) yields.

$$-\frac kmdt=\frac{dv_x}{v_x}$$

Taking the moment when the bullet is fired as moment 0, the component of the initial velocity in the x direction is $v_x$, and the above equation is integrated as follows

$$\int_0^t-\frac kmdt=\int_{v_{x_0}}^{v_x}\frac{dv_x}{v_x}\tag{2}$$

Solving from equation (2) yields.

$$v_x=\frac{dx}{dt}=v_{x_0}e^{-\frac kmt}$$

Integrating both sides of the above equation yields.

$$x=\frac mk v_{x_0}(1-e^{-\frac kmt})\tag{3}$$

Also, the resistance of the bullet in the z-axis direction can be found as

$$f_z=-kv_z-mg=m\frac{dv_z}{dt}$$

The differential equation is obtained by rectifying

$$\frac{dv_z}{dt}+\frac kmv_z+g=0\tag{4}$$

The solution yields.

$$z=\frac km\left(v_{z_0}+\frac{mg}k\right)\left(1-e^{-\frac kmt}\right)-\frac{mg}kt\tag{5}$$

Target point motion model: let the starting position of the target point be $\left(x_{t_0} , z_{t_0}\right)$, the velocity of the target point in the x-axis direction is $v_{t_x}$ and in the z-axis direction is $v_{t_z}$, the component of the actual position of the target point in the x-axis direction is $x_t$ and in the z-axis direction is $z_t$. Following the equation of uniform linear motion, it is obtained that

$$x_t=x_{t_0}+v_{t_x}t\\z_t=z_{t_0}+v_{t_z}t$$

Based on the derivation of the above 2D model, with y denoting the component of the bullet position vector in the y-axis direction and $v_{y_0}$ denoting the component of $v_0$ in the y-axis; the component of the actual position of the target point in the y-axis direction is $y_t$, the y-axis coordinate of the starting position is $y_{t_0}$, and the velocity in the y-axis direction is $v_{t_y}$, the motion model of the bullet and the target point in the y-direction under the 3D model can be obtained as follows

$$y = \frac mkv_{y_0}(1-e^{-\frac kmt})$$

$$y_t = y_{t_0} + v_{t_y}t$$

Code implementation

Base class

template<typename T>
class BulletSolver {
 public:
  BulletSolver(T resistance_coff, T g, T delay, T dt, T timeout) :
      resistance_coff_(resistance_coff),
      dt_(dt), g_(g), delay_(delay),
      timeout_(timeout) {};
  virtual ~BulletSolver() = default;
  virtual void setTarget(const T *pos, const T *vel) = 0;
  virtual void setBulletSpeed(T speed) { bullet_speed_ = speed; }
  virtual void solve(const T *angle_init) = 0;
  virtual void output(T *angle_solved) = 0;
 protected:
  T bullet_speed_{};
  T resistance_coff_, g_, dt_, timeout_, delay_;
};

The BulletSolver class is the base class for all models and algorithms, defining the interface to the algorithm functions that implement the solution to the bullet launch angle, and the member variables such as air resistance coefficient, gravitational acceleration, launch delay, and bullet speed.

function functions

• setTarget()

  setTarget(), used to initialize the initial position and speed of the target.

• setBulletSpeed()

  Set the bullet speed, used to initialize the bullet launch speed.

• solve()

  compute, used to solve the final barrel angle

• output()

  output, used to output the final barrel angle

Variable Description

• bulletspeed(T)

  Initial velocity of the bullet

• resistancecoff

  Air resistance coefficient

• g_

  gravitational acceleration

• dt_

  Loop iteration timeout

• timeout_

  The condition to exit the loop, when the calculated time of the bullet in the air exceeds this value

• delay_

  Barrel firing delay

Bullet motion model

rt_bullet_rho = (1 / this->resistance_coff_) * bullet_v_rho
        * (1 - std::exp(-this->fly_time_ * this->resistance_coff_));

rt_bullet_z = (1 / this->resistance_coff_)
      * (bullet_v_z + this->g_ / this->resistance_coff_)
      * (1 - std::exp(-this->fly_time_ * this->resistance_coff_))
      - this->fly_time_ * this->g_ / this->resistance_coff_;

Variable Description

• bullet_v_rho(T)

  Superposition of bullet velocity $v_x$ and $v_y$

• rt_bullet_rho

  Superposition of the actual position of the bullet in the x-axis component and in the y-axis component

• rt_bullet_z

  The actual position of the bullet in the z-axis component

• flytime

  The time of flight of the bullet

Target point motion model

rt_target_x += this->target_dx_ * this->dt_;
rt_target_y += this->target_dy_ * this->dt_;

Variable Description

• rt_target_x(T)

  The actual position of the target point in the x-axis component

• rt_target_y

  The actual position of the target point in the y-axis component

• targetdx

  target point velocity in x-axis component

• targetdy

  Target point velocity in y-axis component

Please refer to bullet_solver.cpp for the implementation of all algorithms

Test program

Include header files

## Include <iostream>
### Include "bullet_solver.h"

The header file contains the definitions of all classes and functions.

Create class object instances

int main(int argc, char **argv) {
  Iter2DSolver<double> iter2d(0.1, 9.8, 0.01, 0.0001, 3.);
  Approx2DSolver<double> approx2d(0.1, 9.8, 0.01, 0.01, 3.);
  Iter3DSolver<double> iter3d(0.1, 9.8, 0.01, 0.0001, 3.);
  Approx3DSolver<double> approx3d(0.1, 9.8, 0.01, 0.0001, 3.);

Variable Description

• iter2d(Iter2DSolver)

  Instance of the iterative algorithm class object for the 2D model

• approx2d(Approx2DSolver)

  An instance of the velocity superposition algorithm class object for the 2D model

• iter3d(Iter3DSolver)

  3D model of the iterative algorithm class object instance

• approx3d(Approx3DSolver)

  Velocity superposition algorithm class object instance for 3D models

Set parameters

Here is an example of the iterative algorithm for 3D models

  double angle_init[2]{}, angle_solved[2]{};
  double bullet_speed = 18..;
  double pos_3d[3] = {7, 0, 1};
  double vel_3d[3] = {0, 1, 0};
  iter3d.setBulletSpeed(bullet_speed);
  iter3d.setTarget(pos_3d, vel_3d);

Parameter description

• angle_init(double)

  Custom initial launch angle

• angle_solved(double)

  The calculated launch angle

• bullet_speed(double)

  The initial velocity of the bullet

• pos_3d(double[])

  Initial coordinates of the target point

• vel_3d(double[])

  velocity of the target point in the x, y, z directions

Calculate and output the launch angle

  iter3d.solve(angle_init);
  iter3d.output(angle_solved);
  std::cout << "yaw:" << angle_solved[0] << " pitch:" << angle_solved[1] << std::endl;