Skip to main content

枪管角解算器

概述​

在实际中，要打击的目标往往是会移动的，并且子弹在空气中也会受到阻力以及枪管的发射会存在延时。我们需要做一个枪管角度解算器，用于预测枪管的发射角度，从而实现更加精准的打击。

目的:

  • 考虑空气阻力(与速度成正比)
  • 考虑目标速度
  • 考虑发射延时

难点：

  • 无解析
  • 目标解算频率大于 1Khz

两种算法：

  • 迭代法
    • 优点：精度较高(迭代次数多时)
    • 缺点：速度慢
  • 速度叠加法
    • 优点：速度快(20us 内)
    • 缺点：存在固有误差
  • 算法框图：

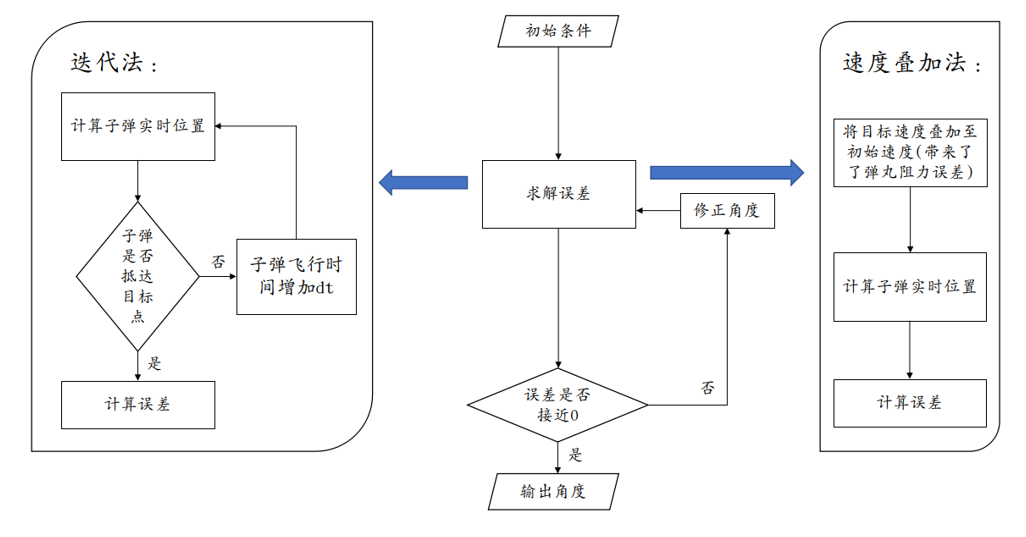
BE2uFg.png

模型推导​

空气阻力与速度成正比，目标点以恒定速度运动 2D 子弹运动模型：在 xz 平面内，假设以子弹子弹发射点为坐标原点，则子弹的实际位置相当于在 xoz 平面内的一个矢量。 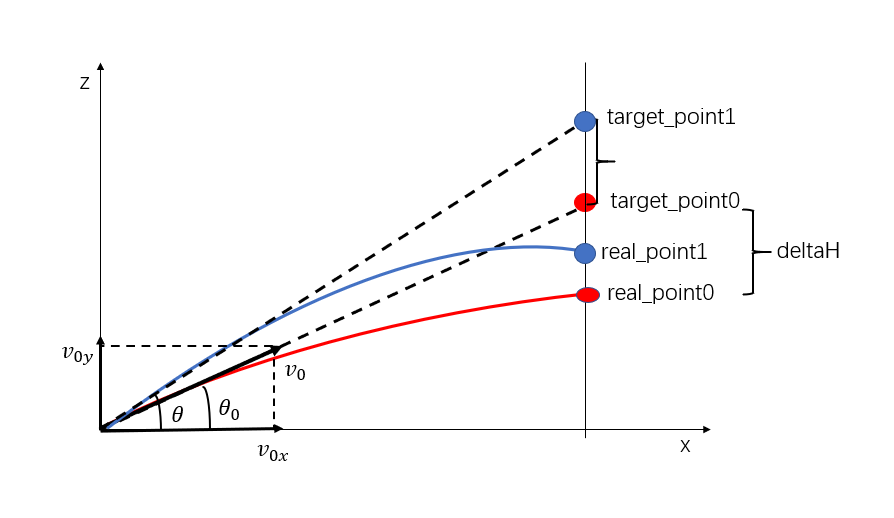BEgFbT.png 用 x 表示子弹位置矢量在 x 轴方向上的分量，用 z 表示子弹位置矢量在 z 轴方向上的分量；v0v_0表示子弹发射初速度，vx、vzv_x、v_z分别表示子弹速度在 x 轴、z 轴的分量，vx0、vz0v_{x_0}、v_{z_0}分别表示v0v_0在 x 轴、z 轴的分量，k 为空气阻力系数，g 为重力加速度，m 表示子弹重量，fxf_x表示子弹所受空气阻力在 X 方向上的分量，根据物理知识知：

fx=−kvx=mdvxdt(1)f_x=-kv_x=m\frac{dv_x}{dt}\tag{1}

将(1)式整理得到：

−kmdt=dvxvx-\frac kmdt=\frac{dv_x}{v_x}

以子弹发射的时刻为 0 时刻,发射初速度在 x 方向上的分量为vxv_x，对上式积分：

∫0t−kmdt=∫vx0vxdvxvx(2)\int_0^t-\frac kmdt=\int_{v_{x_0}}^{v_x}\frac{dv_x}{v_x}\tag{2}

由(2)式求解得到：

vx=dxdt=vx0e−kmtv_x=\frac{dx}{dt}=v_{x_0}e^{-\frac kmt}

对上式两边积分可得：

x=mkvx0(1−e−kmt)(3)x=\frac mk v_{x_0}(1-e^{-\frac kmt})\tag{3}

同时，可求子弹在 z 轴方向上受到的阻力为：

fz=−kvz−mg=mdvzdtf_z=-kv_z-mg=m\frac{dv_z}{dt}

整理得到微分方程：

dvzdt+kmvz+g=0(4)\frac{dv_z}{dt}+\frac kmv_z+g=0\tag{4}

解得：

z=km(vz0+mgk)(1−e−kmt)−mgkt(5)z=\frac km\left(v_{z_0}+\frac{mg}k\right)\left(1-e^{-\frac kmt}\right)-\frac{mg}kt\tag{5}

目标点运动模型：设目标点的起始位置为(xt0,zt0)\left(x_{t_0} , z_{t_0}\right)，目标点在 x 轴方向上的速度为vtxv_{t_x}，在 z 轴方向上的速度为vtzv_{t_z}，目标点实际位置在 x 轴方向的分量为xtx_t，在 z 轴方向的分量为ztz_t。跟据匀速直线运动的公式可得：

xt=xt0+vtxtzt=zt0+vtztx_t=x_{t_0}+v_{t_x}t\\z_t=z_{t_0}+v_{t_z}t

基于上述 2D 模型的推导，用 y 表示子弹位置矢量在 y 轴方向上的分量，vy0v_{y_0}表示v0v_0在 y 轴的分量；目标点实际位置在 y 轴方向的分量为yty_t，起始位置的 y 轴坐标为yt0y_{t_0}，在 y 轴方向上的速度为vtyv_{t_y}，可以得到 3D 模型下子弹和目标点在 y 方向的运动模型：

y=mkvy0(1−e−kmt)y = \frac mkv_{y_0}(1-e^{-\frac kmt})
yt=yt0+vtyty_t = y_{t_0} + v_{t_y}t

代码实现​

基类​

template<typename T>
class BulletSolver {
 public:
  BulletSolver(T resistance_coff, T g, T delay, T dt, T timeout) :
      resistance_coff_(resistance_coff),
      dt_(dt), g_(g), delay_(delay),
      timeout_(timeout) {};
  virtual ~BulletSolver() = default;
  virtual void setTarget(const T *pos, const T *vel) = 0;
  virtual void setBulletSpeed(T speed) { bullet_speed_ = speed; };
  virtual void solve(const T *angle_init) = 0;
  virtual void output(T *angle_solved) = 0;
 protected:
  T bullet_speed_{};
  T resistance_coff_, g_, dt_, timeout_, delay_;
};

BulletSolver 类是所有模型以及算法的基类，定义了实现求解子弹发射角度的算法函数接口，和空气阻力系数、重力加速度、发射延时、子弹速度等成员变量。

函数功能​

  • setTarget()

    设置目标点，用于初始化目标点初始位置及速度

  • setBulletSpeed()

    设置子弹速度，用于初始化子弹发射速度

  • solve()

    计算，用于解算最终的枪管角度

  • output()

    输出，用于输出最终枪管角度

变量说明​

  • bulletspeed(T)

    子弹初速度

  • resistancecoff

    空气阻力系数

  • g_

    重力加速度

  • dt_

    循环迭代时间间隔

  • timeout_

    退出循环的条件，当计算到子弹在空中飞行的时间超过此值时将退出循环

  • delay_

    枪管发射延时

子弹运动模型​

rt_bullet_rho = (1 / this->resistance_coff_) * bullet_v_rho
        * (1 - std::exp(-this->fly_time_ * this->resistance_coff_));

rt_bullet_z = (1 / this->resistance_coff_)
      * (bullet_v_z + this->g_ / this->resistance_coff_)
      * (1 - std::exp(-this->fly_time_ * this->resistance_coff_))
      - this->fly_time_ * this->g_ / this->resistance_coff_;
变量说明​

  • bullet_v_rho(T)

    子弹速度vxv_x与vyv_y的叠加

  • rt_bullet_rho

    子弹实际位置在 x 轴分量和在 y 轴分量的叠加

  • rt_bullet_z

    子弹实际位置在 z 轴分量

  • flytime

    子弹的飞行时间

目标点运动模型​

rt_target_x += this->target_dx_ * this->dt_;
rt_target_y += this->target_dy_ * this->dt_;
变量说明​

  • rt_target_x(T)

    目标点实际位置在 x 轴分量

  • rt_target_y

    目标点实际位置在 y 轴分量

  • targetdx

    目标点速度在 x 轴分量

  • targetdy

    目标点速度在 y 轴分量

所有算法具体实现请参考bullet_solver.cpp

测试程序​

包含头文件​

#include <iostream>
#include "bullet_solver.h"

头文件中包含所有类、函数的定义。

创建类对象实例​

int main(int argc, char **argv) {
  Iter2DSolver<double> iter2d(0.1, 9.8, 0.01, 0.0001, 3.);
  Approx2DSolver<double> approx2d(0.1, 9.8, 0.01, 0.01, 3.);
  Iter3DSolver<double> iter3d(0.1, 9.8, 0.01, 0.0001, 3.);
  Approx3DSolver<double> approx3d(0.1, 9.8, 0.01, 0.0001, 3.);
变量说明​

  • iter2d(Iter2DSolver)

    2D 模型的迭代算法类对象实例

  • approx2d(Approx2DSolver)

    2D 模型的速度叠加算法类对象实例

  • iter3d(Iter3DSolver)

    3D 模型的迭代算法类对象实例

  • approx3d(Approx3DSolver)

    3D 模型的速度叠加算法类对象实例

设置参数​

这里以 3D 模型的迭代算法为例

  double angle_init[2]{}, angle_solved[2]{};
  double bullet_speed = 18.;
  double pos_3d[3] = {7, 0, 1};
  double vel_3d[3] = {0, 1, 0};
  iter3d.setBulletSpeed(bullet_speed);
  iter3d.setTarget(pos_3d, vel_3d);
参数说明​

  • angle_init(double)

    自定义的初始发射角度

  • angle_solved(double)

    计算得出的发射角度

  • bullet_speed(double)

    子弹发射初速度

  • pos_3d(double[])

    目标点初始坐标

  • vel_3d(double[])

    目标点在 x、y、z 方向上的速度

计算并输出发射角​

  iter3d.solve(angle_init);
  iter3d.output(angle_solved);
  std::cout << "yaw:" << angle_solved[0] << " pitch:" << angle_solved[1] << std::endl;